













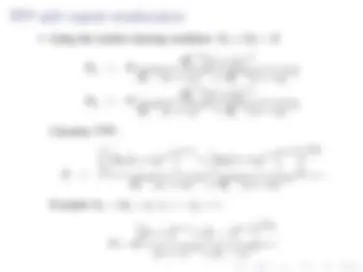








Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
Lecture Notes for the financial part of the course.
Typology: Lecture notes
1 / 31

This page cannot be seen from the preview
Don't miss anything!















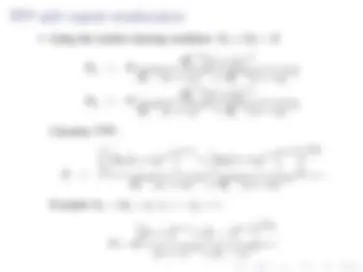








Shengxing Zhang
September 26, 2017
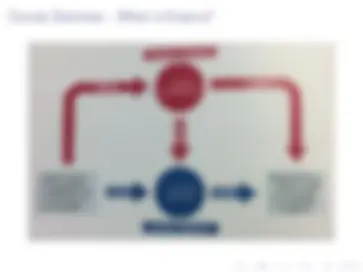
I (^) Alice
I (^) receives today £100,
I (^) save £100 in a bank
I (^) receives next year £
I (^) Bob
I (^) needs £100 to buy seeds and borrows from the bank
I (^) sell plants for £110 next year
I (^) repays £101 to the bank
I (^) Social surplus generated by the financial contract
I (^) £110-£100=£
I (^) Financing investment
I (^) Financial market ( equity, bond, etc)
I (^) Financial intermediaries ( loan )
I (^) Sharing risk through financial institutions
I (^) Mutual funds in the financial market
I (^) Commercial banks
I (^) Overcoming asymmetric information
I (^) Moral hazard: hidden knowledge of actions
I (^) Lemon: hidden knowledge of attributes
I (^) Fostering growth
I (^) reduce capital misallocation
I (^) Contributing to fluctuations over the business cycle
I (^) financial crisis
I (^) economic boom
I (^) Key: incompleteness of the financial market and resulting
inefficiency
I (^) Suppose that the production function is an economy is
f ( k |{z}
capital
, l |{z}
labor
|{z}
other input
I (^) Imagine that the society produces output using an aggregate
production function
|{z}
Total Output
= Af ( K |{z}
Total Capital Supply
|{z}
Total Labor Supply
where A is the total-factor productivity (TFP)
I (^) But the production of the society is operated by many
individual firms
i
Ai f (ki , li ,.. .)
So the allocation of resources may affect the productivity of
the economy.
Productivity
i
Ai f (ki , li ,.. .)
f (K , L,.. .)
Suppose the production function is f (k) = k.
I (^) Under utilization of capital.
There is only one firm in the economy but the demand of
capital from the firm is K � �. So, the output of the economy
is K � �.Then the productivity of the economy is 1 �
�
K
I (^) Allocation of resources across firms.
Suppose there are N firms. There is no financial market to
reallocate capital. Firm i produces Ai ki units of output. The
productivity of the economy is
N X
i= 1
Ai
ki P
j
kj
I (^) An equilibrium is consumption of the household c, firms’ labor
demand, l 1 , l 2 , firms’ profit ⇡ 1 , ⇡ 2 and wage w , such that
I (^) Given w , l i solves firm^ i’s problem.
I (^) The labor market clears 1 = l 1 +^ l 2.
I (^) c = ⇡ 1 +^ ⇡ 2 +^ w^.
I (^) From the firm’s optimization problem, l i =^ ki
h Ai ( 1 �↵)
w
i 1 /↵
I (^) From the market clearing condition, l 1 +^ l 2 =^ 1. We have
w =
i
ki [Ai ( 1 � ↵)]
1 /↵
↵
I (^) The output of the economy is
i
Ai k
↵ i
l
1 �↵
i
i
Ai k
↵ i
ki A
1 /↵
i P
j
kj A
1 /↵
j
1 �↵
I (^) TFP of the economy (let K ⌘
i
ki )
i
Ai k
↵
i
l
1 �↵
i
↵
i
Ai
ki
ki A
1 /↵
i P
j
kj A
1 /↵
j
1 �↵
maxY 1 ,Y 2 ,K 1 ,K 2
�� 1 � 1
�� 1 � 2
�� 1
subject to Y 1 = A 1 K 1 , Y 2 = A 2 K 2 ,
Lagrangian
�� 1 � (^) + (A 2 K 2 )^
�� 1 � (^) + �(K � K 1 �^ K 2 )
First order condition:
�� 1 � (^) � �
�� 1 � (^) � �
�� 1
�� 1 1
�� 1 1
�� 1 2
�� 1 2
�� 1
1
�� 1
2
I (^) Two types of firms, producing intermediary goods of type one
and type two
I (^) A market for renting capital
I (^) The representative household owns the capital stock
maxY 1 ,Y 2
�� 1 � 1
�� 1 � 2
�� 1
subject to P 1 Y 1 + P 2 Y 2 = RK + ⇡ 1 + ⇡ 2
�Pi = Y
�
1 � i
�� 1 � 1
�� 1 � 2
�� 1
Normalize the price of the general good so that
Pi (Yi ) = CY
�
1 �
i
where C =
�� 1 � 1
�� 1 � 2
�� 1
.
An equilibrium is interest rate R and capital allocation K 1 and K 2
such that
I (^) Given interest rate R, K 1 and^ K 2 solve the profit maximization
problem firm 1 and firm 2
I (^) The demand function solves the representative agent’s
consumption given any price, P(Yi )
I (^) Capital market clears
From the profit maximization problem of firms
�� 1
1
�
�� 1 2
�
�� 1
Using the market clearing condition K 1 + K 2 = K
�� 1
1
�� 1
1
�� 1
2
�� 1
2
�� 1
1
�� 1
2
The decentralized equilibrium implements the first best allocation.