1
4.4: Composite Numerical
Integration
Prepare for your exams
Study with the several resources on Docsity
Earn points to download
Earn points by helping other students or get them with a premium plan
Guidelines and tips
Prepare for your exams
Study with the several resources on Docsity
Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community
Ask the community for help and clear up your study doubts
University Rankings
Discover the best universities in your country according to Docsity users
Free resources
Our save-the-student-ebooks!
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
Composite Numerical Integration: Overcoming Large Intervals with Simpson's Rule, Slides of Calculus
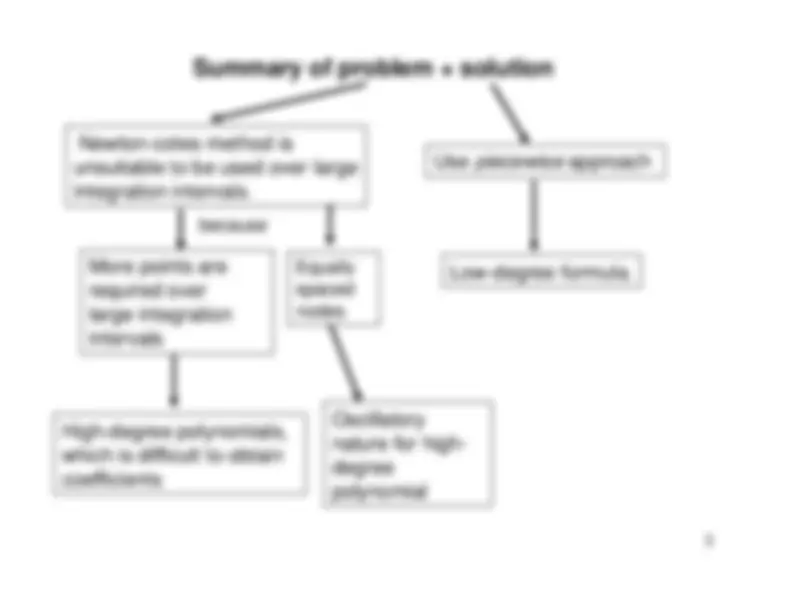
The challenges of using Newton-Cotes methods, specifically Simpson's Rule, for large integration intervals. The text suggests a piecewise approach, dividing the interval into subintervals and applying Simpson's Rule to each one. The document also introduces the concept of Generalized Simpson's Rule and provides an algorithm for its implementation.
Typology: Slides
2021/2022
1 / 14
This page cannot be seen from the preview
Don't miss anything!
Related documents
Partial preview of the text
Download Composite Numerical Integration: Overcoming Large Intervals with Simpson's Rule and more Slides Calculus in PDF only on Docsity!
4.4: Composite Numerical
Integration
Problem arising from large
integration interval
-^
Use Simpson’s Rule
(^76958). 56 )
4
2 ( 3
4 2
0
(^40) 1
=
∫^
=
=^
e e
e
dx e
f^
x
Analytical Solution:
(^59819). 53 0
4
(^40)
2
=
−
=
∫ =^
e
e
dx e
f^
x
(^17143). 3 |
|^
2 1
=
−
=
f f
error
)] ( )( 4 ) ([ 3 )(
2 1 0
(^20)
xf xf
xf h dxx x f x^
≈
Solution:
piecewise
technique (divide [0,4] into
several subinterval) e.g. [0,4]= [0,1]+ [1,2]+ [2,3]+ [3,4]and use Simpson’ rule (
,^ i.e. low-order
Newton-Cotes
) in each subinterval. (^61622). 53
2 3 2
1 2 4 0 0
(^10)
(^21)
(^32)
(^43)
=^ ∫
∫^
∫^
∫^
∫ e e e e e e
dx e
dx e
dx e
dx e
dx e
f^
x
x
x
x
x
(^01807). 0 |
|^
2 3
=
−
=^
f f
error
)]( )( (^4) ) ([ 3 )(
2 1 0
(^20)
xf xf xf h dxx x fx^
≈ ∫
Generalized Simpson’s rule using
piecewise
(composite)
method
y
x^0 a^ =
x^^1
... x 2
(^22) − j x^
(^12) − j x^
... x 2 j
xn b^ =
y=f(x)^ x
jh a x
n a b h
n
j j^
=
−
−
=
/) (
(^1) ) (^2) / ,....( (^1) , 0
Remarks for the method: zApplication at each subinterval. So
n^ has to be
even, i.e. total number of points is
n+
.
zPoints at
j=2, 4,…2j
are used twice.
) ( 2 90 ) (^
4
5
μ f n h
f E^
× − =^
) (
180
)
(^
4 4
μ f h a b^
− − =
ab n
h^
) (^ − =
Algorithm (for Composite Simpson’s Rule) Input:Output:
)] ( ) ( 4 ) ( 2 ) (
[ 3
2 1
1 2
12 1
2
0
n
n j^
j
n j^
j^
x f x f x f x f h
I^
∑
∑
=^
=^
−
− =
n b a^
, ,^
e SUM
0 SUM
Step 1: set
n
a
b
h^
(^
Step 2:
0 = e
SUM
0 = 0
SUM
initialize
Step 3: For
do steps 4, 5
Summationgetand
0 SUM SUM
e
Step 4:
ih a X^
1
,....... 1
−
=^
n
i
Step 5: If
is even
else
i^
) (^ Xf
SUM SUM
e e^
=
) ( 0
0
X f
SUM
SUM
=
looping
Step 6:
)] (
) ( [ 3
0
b f
SUM
SUM a f h I^
e^
=
Step 7: Output
I
(^
2
1 1
μ
f
ah
b b f x f a f h
dx
x
b fa
n j^
j^
∫^
⎡^ ⎢⎣
=^
− =
) ( 3 ) ( 2 ) (
3
1
0
f h
x hf
dx x f x x^
′′
∫^
=
−
Midpoint rule.
Trapezoidal
(^1) − =^ xa
x^^0
x^^1
1 x^^2 − j
j x^2
1 x^^2 + j
(^1) +
=^
xn
b
xn
open interval
•Example: Use both Composite Simpson’s ruleand Composite Trapezoidal rule toapproximate
with n=
π ∫ 0
sin
xdx
Simpson’s composite rule:
sin( 4 ) 10 sin( 2 60
sin
sin(
sin 4
sin
2 ) 0 sin( 3
sin
9 1
10 1
0 0
(^1) ) (^2) / (
1
(^2) / 1
1 2
2
⎤^ =⎥ ⎦
⎡^ ⎢ ⎣
⎡^ ⎢ ⎣
∑
∑
∫^ ∫
∑
∑
=^
= − =
=
−
j^
j j n j
n j
j
j
j
j
xdx
n
j jh a x n a b h
x
x
h xdx
π
π
π
π
π
π π
Trapezoidal composite rule:
(^9958860). 1 ) 20 sin( 2 40 ) sin 0 sin ) 20 sin( (^2) [ 40
sin
(^20) /
(^20) /)
( , 20
19 1
0
19 1
⎤^ =⎥ ⎦
⎡ ⎢ ⎣
≈
=
−
=
∑
∫^
∑
=
=^
j
j
j
j
xdx
a b h n
π
π π
π
π
π
π