







Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
Examples and solutions for determining the tensions in cables of coplanar force systems in equilibrium. It covers the drawing of free body diagrams, application of equations of equilibrium, and solving for unknown forces. several examples with given weights and geometries, and provides the steps to find the forces in the cables.
What you will learn
Typology: Study notes
1 / 10

This page cannot be seen from the preview
Don't miss anything!







This is an example of a 2-D or coplanar force system. If the whole assembly is in equilibrium, then particle A is also in equilibrium. To determine the tensions in the cables for a given weight of the engine, we need to learn how to draw a free body diagram and apply equations of equilibrium.
If a particle is subjected to a system of coplanar forces that lie in
components. For equilibrium,
For this vector equation to be satisfied, both the x andy components must be equal to zero. Hence,
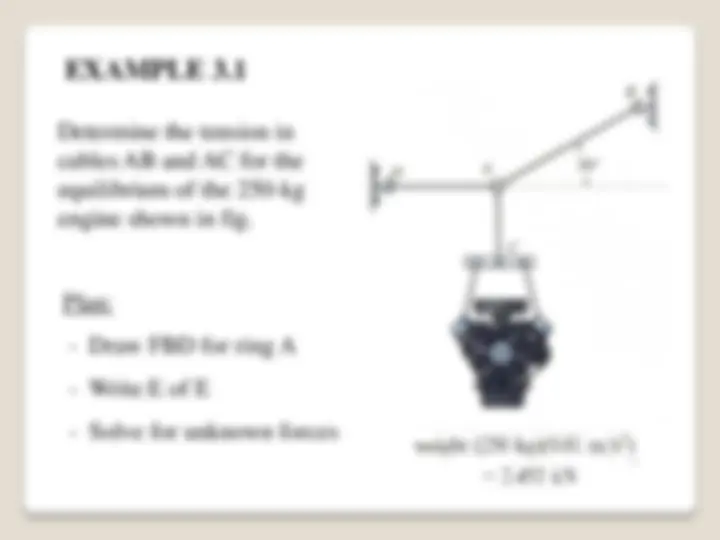
Determine the tension in cables AB and AC for the equilibrium of the 250-kg engine shown in fig.
Plan:
Write the scalar E of E:
Fx = TB cos 30º – TD = 0
Fy = TB sin 30º – 2. 452 kN = 0
Solving the second equation gives:
TB = 4. 90 kN
From the first equation, we get:
TD = 4. 25 kN
FBD at A
EXAMPLE 3.2 (continued)
The scalar E-of-E are:
Solving these two simultaneous equations for the two unknowns yields:
TEC = 38. 6 lb TEG = 54. 6 lb
A FBD at E should look like the one to the left. Note the assumed directions for the two cable tensions.
Fx = 38. 64 cos 45 – (4/5) TCD = 0 Fy = (3/5) TCD + 38.64 sin 45 – WB = 0
Solving the first equation and then the second yields
TCD = 34. 2 lb and WB = 47. 8 lb.
The scalar E-of-E are:
Now move on to ring C. A FBD for C should look like the one to the left.
EXAMPLE 3.2 (continued)
PROBLEM SOLVING (continued)
25 °^30 °
600 lb
FBD at point A
Applying the scalar E-of-E at A, we get;
Fx = FAC cos 30° – FAB cos 25° = 0
Fy = -FAC sin 30° – FAB sin 25° + 600 = 0
Solving the above equations, we get;
FAB = 634 lb
FAC = 664 lb